PCA by Python

Table of Contents

1. Introduction
#

This article records two methods of PCA analysis using Python, and visualizes 2-dimensional results

1.1 What’s PCA?
#

When it comes to methods of reducing dimension, PCA that is an unsupervised linear transformation technique, must be not ignored. Moreover, if you want to know the subtle relationships among data set and reduce the computational complexity in downstream analysis, the PCA may be your best choice! Meanwhile, if you would like to present your data in a 2-dimension or 3-dimension coordinate system, and PCA would sweep your problems!

What is reducing dimension? I will show you an example as follows: First, suppose you have a five-dimensional data set :

Id	1-d	2-d	3-d	4-d	5-d
data-1	1	2	3	4	5
data-2	6	7	8	9	10
..	..	..	..	..

Then, you could pick up PC1 and PC2 after PCA to reduce dimension for plotting:

Id	PC1	PC2
data-1	0.3	0.6
data-2	0.1	1.2
..	..	..

PC1 and PC2 are the result obtained through data is projection on the unit vectors, which enable result to have the biggest variance(means its distribution is wide) and to be irrelevant(covariance = 0).

1.2 Algorithm
#

Normalize $d$ dimension raw data
Create the covariance matrix
Calculate the eigenvalues of the covariance matrix and the corresponding eigenvectors
The eigenvectors are sorted in the matrix according to the corresponding feature value, and the first k rows are formed into a matrix $W$. ($k<<d$)
$Y = xW$ is the result after reducing dimension to k dimension

Note: There are two prerequisites for conducting PCA

Raw data has no NA
The raw data should be normalized

2. PCA from scratch
#

Importing necessary modules

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

Creating raw data

# get  data set
df_wine = pd.read_csv(
    "http://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data",
    header=None,
    engine="python",
)
# check data
df_wine.head()

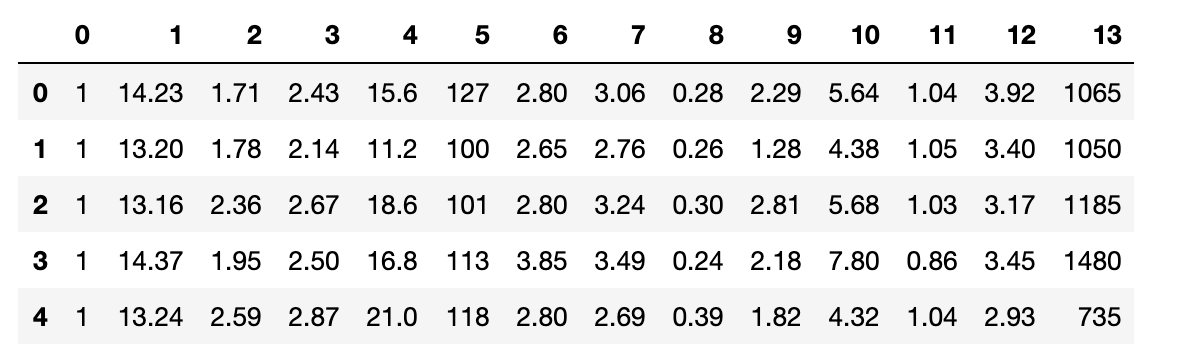
Creating train and test data set

# create train and test data set

X, y = df_wine.iloc[:, 1:], df_wine.iloc[:, 0]

x_train, x_test, y_train, y_test = train_test_split(
    X, y, test_size=0.3, stratify=y, random_state=0
)

Standardizing the features

# create standard instance
sc = StandardScaler()
# standard data
x_train_std = sc.fit_transform(x_train)
x_test_std = sc.fit_transform(x_test)

Creating the covariance matrix and Getting eigenvectors and eigenvalues

the calculation of the covariance matrix :

$$ \sigma_{jk} = \frac{1}{n} \sum^{n}_{i=1}\bigg(x_{j}^{(i)} - \mu_j\bigg)\bigg(x_{k}^{(i)} - \mu_k\bigg) $$

Then, using numpy.cov and numpy.linalg.eig to get the covariance matrix and eigenvectors respectively

# calculate the covariance matrix
cov_mat = np.cov(x_train_std.T)
# Getting eigenvectors and eigenvalues
eigen_vals, eigen_vecs = np.linalg.eig(cov_mat)

NOTE: there are 13 eigenvectors totally, the number of eigenvalues might be not as same as the number of features sometimes.

Firstly, plotting the Variance interpretation ratio, which is obtained through eigenvalue $\lambda_j$ divided by the sum of all the eigenvalues:

$$ \frac{\lambda*j}{\sum^d_{j=1}\lambda_j} $$

# get sum of all the eigenvalues
tot = sum(eigen_vals)
# get variance interpretation ratio
var_exp = [(i / tot) for i in sorted(eigen_vals, reverse=True)]
cum_var_exp = np.cumsum(var_exp)

Besides, plotting the result to get in-depth understanding:

plt.figure()  # create plot
# create bar plot
plt.bar(
    range(1, 14),
    var_exp,
    alpha=0.5,
    label="individual explained variance",
)
# create step plot
plt.step(range(1, 14), cum_var_exp, where="mid", label="cumulative explained variance")
# add label
plt.ylabel("Explained variance ratio")
plt.xlabel("Principal component index")
# add legend
plt.legend(loc="best")
# save picture
plt.savefig("pca_index.png", format="png", bbox_inches="tight", dpi=300)

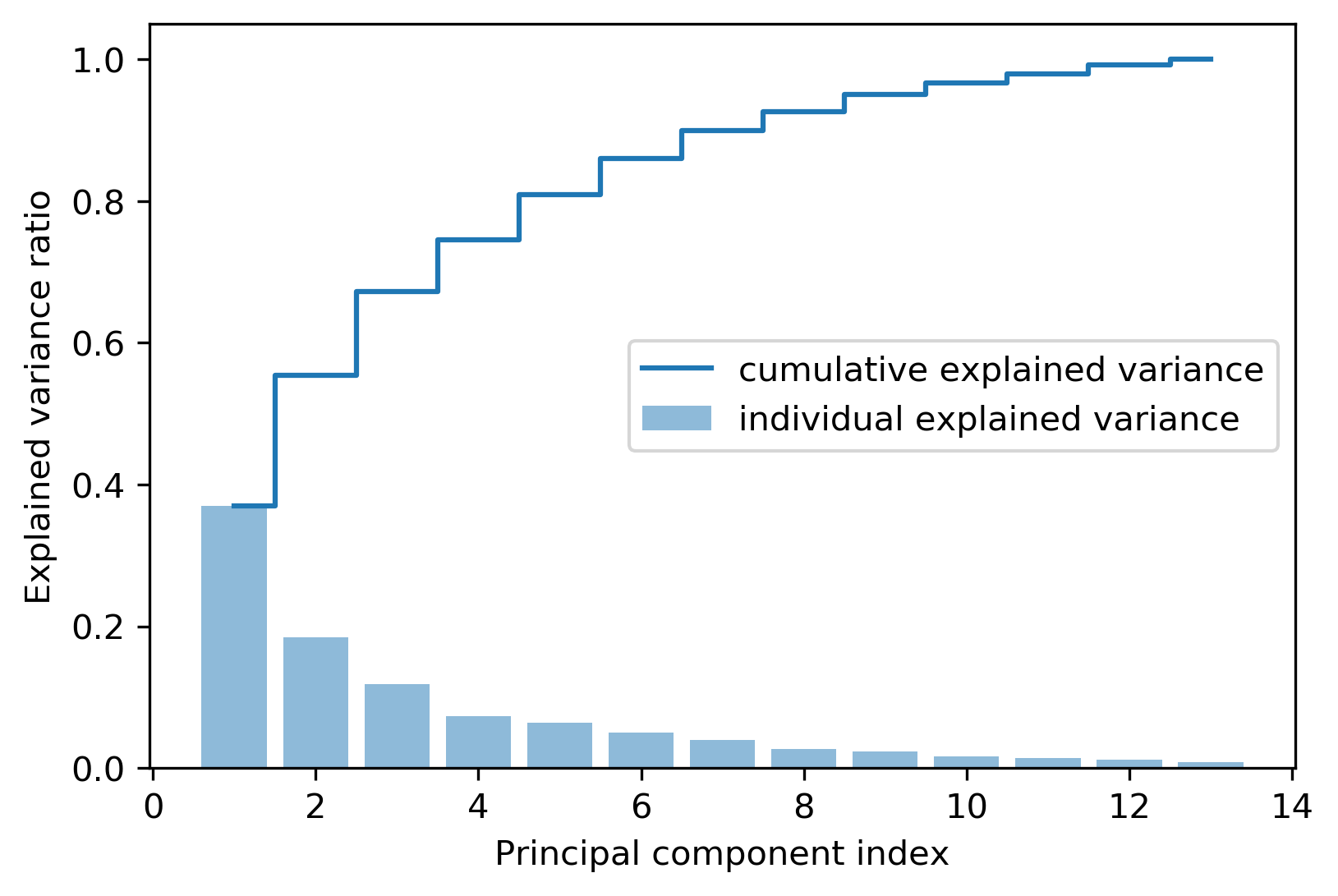
We can conclude that PC1 only takes account for about 40%. Furthermore, the sum of PC1 and PC2 have 60% variance.

Selecting the first k values to form matrix $W$

# integrate eigenvalues  and eigenvectors
eigen_paris = [
    (np.abs(eigen_vals[i]), eigen_vecs[:, i]) for i in range(len(eigen_vals))
]
# sort according to eigenvalues
eigen_paris.sort(key=lambda x: x[0], reverse=True)
# pick up the first 2 eigenvalues
w = np.hstack([eigen_paris[0][1][:, np.newaxis], eigen_paris[1][1][:, np.newaxis]])
# check matrix x
w

Transforming raw data

# reduce dimension
x_train_pca = x_train_std.dot(w)
# check resulted data
x_train_pca.shape

(124, 2)

Then plotting the result and putting the label in terms of original info, but keeping in mind PCA is unsupervised learning skill without labels

# init colors and markers
colors = ["r", "b", "g"]
markers = ["s", "x", "o"]
# plot scatter
for l, c, m in zip(np.unique(y_train), colors, markers):
    plt.scatter(
        x_train_pca[y_train == l, 0],
        x_train_pca[y_train == l, 1],
        c=c,
        label=1,
        marker=m,
    )
# add label and legend
plt.xlabel("PC 1")
plt.ylabel("PC 2")
plt.legend(loc="lower left")
plt.savefig("distribution.png", format="png", bbox_inches="tight", dpi=300)

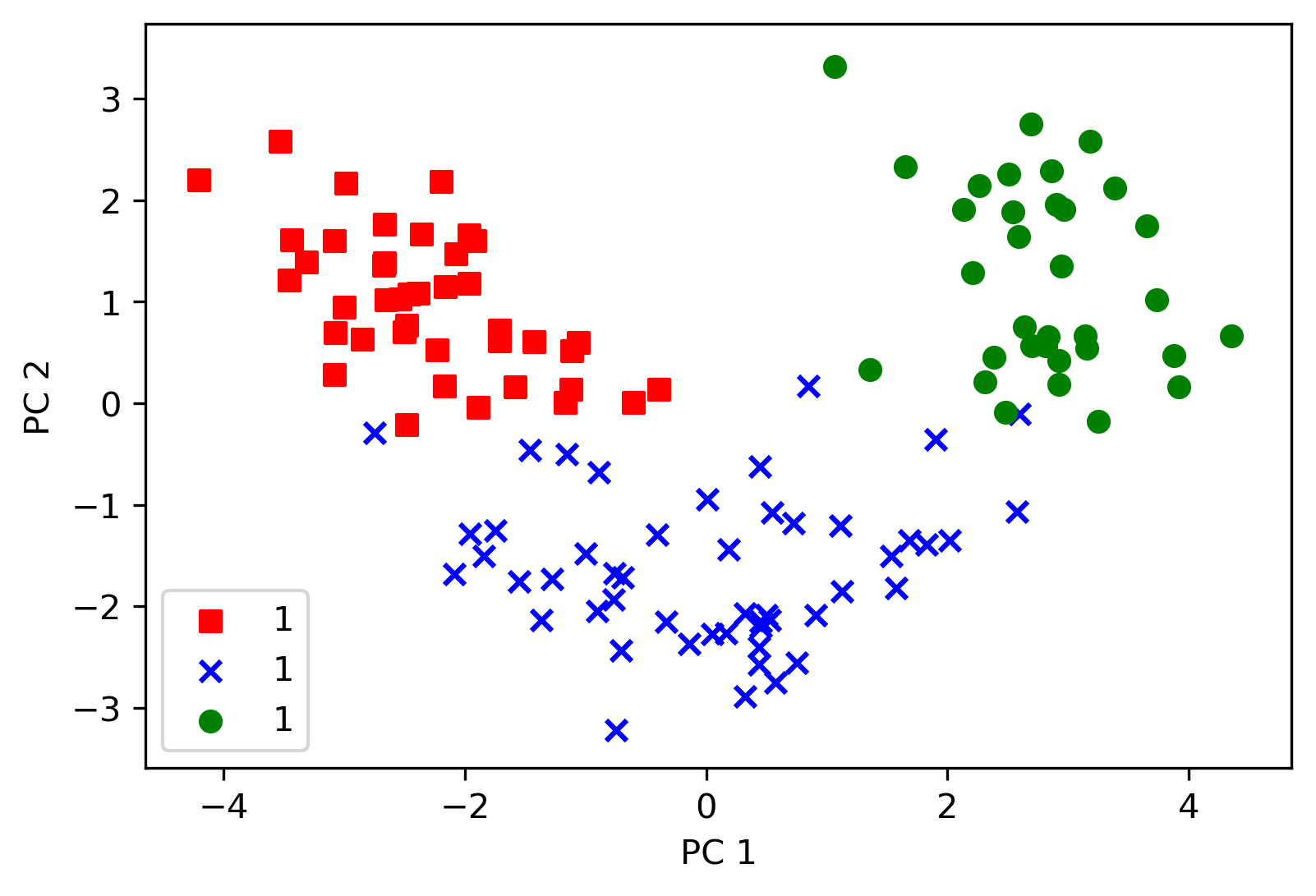
3. PCA by scikit-learn
#

we can conduct PCA easily by sklearn

Importing modules

from sklearn.decomposition import PCA
from matplotlib.colors import ListedColormap
from sklearn.linear_model import LogisticRegression

Defining function of plot_decision_region

def plot_dicision_regions(X, y, classifier, resolution=0.02):
    # init markers and colors
    markers = ("s", "x", "o", "^", "v")
    colors = ("red", "blue", "lightgreen", "gray", "cyan")
    cmap = ListedColormap(colors[: len(np.unique(y))])
    # create info for plot region
    x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx1, xx2 = np.meshgrid(
        np.arange(x1_min, x1_max, resolution), np.arange(x2_min, x2_max, resolution)
    )
    # test classifier's accurate
    z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
    z = z.reshape(xx1.shape)
    # plot decision region
    plt.contourf(xx1, xx2, z, alpha=0.4, cmap=cmap)
    # set x,y length
    plt.xlim(xx1.min(), xx1.max())
    plt.ylim(xx2.min(), xx2.max())
    # plot result
    for idx, cl in enumerate(np.unique(y)):
        plt.scatter(
            x=X[y == cl, 0],
            y=X[y == cl, 1],
            alpha=0.6,
            color=cmap(idx),
            edgecolor="black",
            marker=markers[idx],
            label=cl,
        )

PCA by sklearn

# create pca instance
pca = PCA(n_components=2)
# create classifier instance
lr = LogisticRegression()
# reduce dimension for  data set
x_train_pca = pca.fit_transform(x_train_std)
x_test_pca = pca.transform(x_test_std)
# classify x_train_pca
lr.fit(x_train_pca, y_train)
# plot decision region
plot_dicision_regions(x_train_pca, y_train, classifier=lr)
# add info
plt.xlabel("PC 1")
plt.ylabel("PC 2")
plt.legend(loc="lower left")
plt.show()

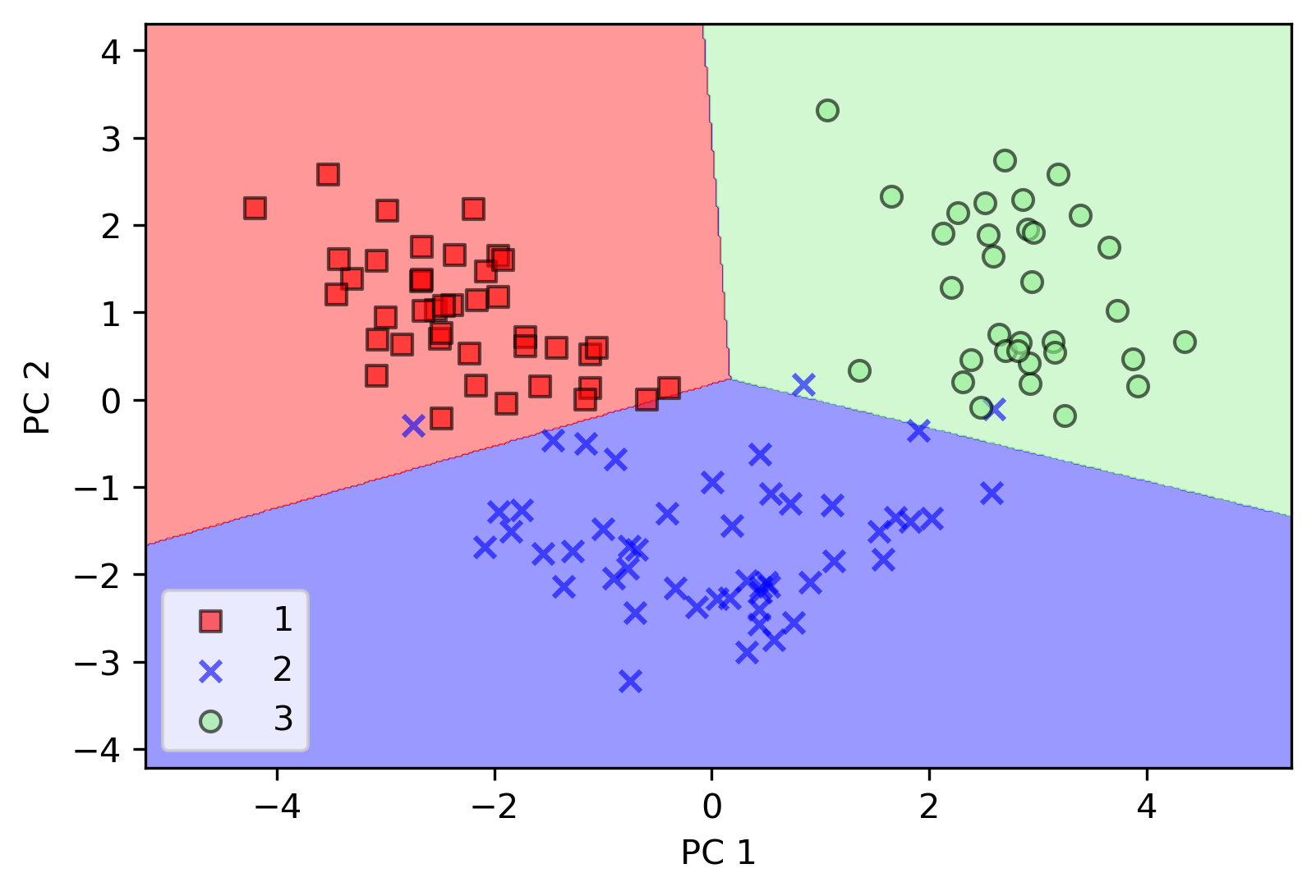
We can see that the classifier’s accurate is excellent according to actual labels

TIPS:

You can set n_components = None, and the result would retain all principle components. Moreover, you could call explained_variance_ration_ to use variance explanation ratio.

3. Summary
#

All the above are the main content, welcome everybody communicates with me! 🤠

Reference book : Python machine learning

1. Introduction#

1.1 What’s PCA?#

1.2 Algorithm#

2. PCA from scratch#

3. PCA by scikit-learn#

3. Summary#